CS231n笔记 Lec4 神经网络

1.神经网络模型

• 生物神经网络中树突(dendrite)作为输入与其他神经元的轴突相连，而轴突作为神经元的输出，人工神经网络有借鉴这个模型。神经网络有输入层、隐层和输出层。

• 人工神经网络仅仅是生物神经网络的一个粗糙模型，比如生物神经网络会有多种类型的神经元，并且每个有着不同属性，树突进行复杂的非线性运算，突触是一个非线性动态系统，并且在精确的时间输出脉冲在许多系统中是重要的，这些在人工神经网络中只进行了简单的建模或者未建模。

• 单个神经元本质上是一个线性分类器（然后通过激活函数来加入非线性因素）。

• 其层数计算不算输入层，比如单层神经网络描述的是一个没有隐层的神经网络。

• 输出层通常不作用激活函数，因为输出层被用来计算分类得分，可以是任意实数。

• 计算神经网络训练的参数个数：

  

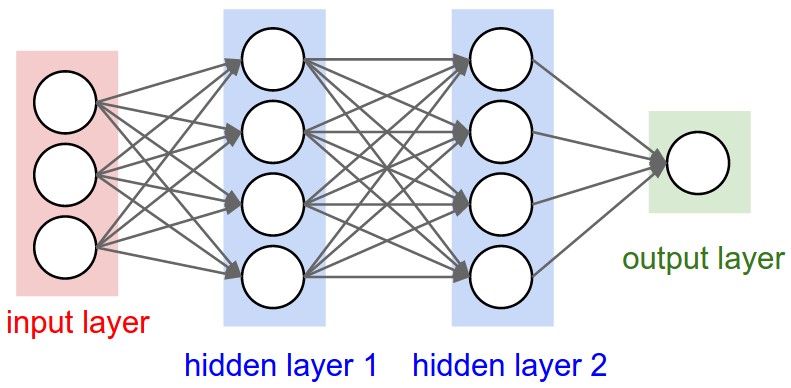
  该神经网络有4+4+1个神经元，权重参数有[3×4] + [4×4] + [4×1] = 32个，加上bias参数4+4+1个，共41个训练参数。

• 单隐层神经网络可以逼近任意连续函数（intuitive explanation），尽管该点在数学上可以证明，但是在实践中是一个相对薄弱或者说无用的条件。相关阅读：

  1）Deep Learning book in press by Bengio, Goodfellow, Courville, in particular Chapter 6.4.

  2）Do Deep Nets Really Need to be Deep?

  3）FitNets: Hints for Thin Deep Nets

2.常见激活函数

• sigmoid函数：由于1）[严重]当激活函数输出值为0或者1时，会导致梯度消失（Gradient Vanishing）,实际上也可以发现sigmoid函数一阶导数的最大值为1/4,所以每经过一次激活函数梯度变为原来的1/4。2）sigmoid函数不是以0为中心的。由于输入数据为正数，sigmoid函数的值也为正数，所以梯度值要么都为正数要么都为负数，这将会导致优化路径为Z字型，效率低，不过这个问题可以通过累加一批次数据的梯度来缓和。

• tanh函数：这个函数同样存在梯度消失问题，实际上tanh函数是一个经过线性变换的sigmoid函数，存在关系$tanh(x) = 2\sigma(2x) - 1$ 。

• ReLU（Rectified Linear Unit）: $\max(0, x)$ ，这个函数近年来常用，有一些支持和反对意见。

  1) + 比起sigmoid和tanh，它被发现有利于加速SGD的收敛，论点是由于该函数是线性的且不饱和（non-saturating）。

  2) + 比sigmoid和tanh，ReLU计算开销更小。

  3) - ReLU unit在训练过程中容易停滞（Dying ReLU），因为当一个较大梯度值通过ReLU神经元导致权重更新后，这个ReLU神经元将很难再被激活。这个问题可以通过调整学习率来缓和。

• Leaky ReLU：$f(x) = \mathbb{I} (x < 0)(\alpha x) + \mathbb{I} (x < 0)(x)$，这么设计的原因主要是为了解决Dying ReLU问题，不过这个函数并没有绝对改善。

• Maxout: $\max (w_1^Tx + b_1, w_2^Tx + b_2)$，可以解决Dying ReLU和 saturating问题，但是由于要对每个神经元需要训练两组参数，使得参数数量增多。

实践指导：实践中同一个神经网络中混合多种神经元十分罕见，尽管这么做没有根本性问题，通常我们使用ReLU函数，如果在意Dying ReLU问题，尝试Leaky ReLU或者Maxout，永远不要使用sigmoid。

3.如何设置神经网络的层数以及每层神经元的个数

• 神经网络的层数和每层神经元的个数越多，神经网络的表示能力越强，但是同时会带来过拟合的问题，实践中并不鼓励为了缓解过拟合问题而降低神经网络的规模，而是通过一些手段（L2 Regularization、Dropout等）来缓和。
• 神经网络规模越小越难被训练，因为其容易陷入不好的局部最小值。

4.数据预处理

• PCA

  • 协方差矩阵： $\Sigma = E\big[(\textbf X - E[\textbf X])(\textbf X - E[\textbf X])^T\big]$，其中矩阵的第(i, j)个元素是$X_i$与$X_j$的协方差，$\Sigma$的对角线是方差。$\Sigma$是对称的和半正定positive semi-definite的。计算方式：

    1
    2
    X -= np.mean(X, axis=0)
    cov = np.dot(X.T, X) / X.shape[0]
    

  • SVD分解：假设$M$是一个m×n阶的矩阵，其元素属于实数域或者复数域，若存在分解

    $$M = U\Sigma V^*$$

    其中$U$是m×m阶的酉矩阵，$\Sigma$是m×n阶非负实数对角矩阵，$V^$ （$V$的共轭转置）为n×n的酉矩阵 （$VV^=\mathbb I_n$），则称这样的分解为奇异值分解。其中$\Sigma$的对角线元素为$M$的奇异值。

    1
    2
    U,S,V =  np.linalg.svd(cov)
    Xrot = np.dot(X, U)
    

    其中U的每一列是特征向量，S是一维向量奇异值。

  将X与U的若干列做点积就是PCA。

• Whitening(白化)：

  1
  Xwhite = Xrot / np.sqrt(S + 1e-5)
  

  该方法会放大噪声，实践中可以增大1e-5来减少噪声影响。

  卷积神经网络中PCA/Whitening都不使用，使用mean和normalization。

• 权重不能都初始化为0，因为如果权重都初始化为同一个数，则他们更新时计算的梯度也是一样的，从而导致训练后的参数都相同。通常采用随机初始化。

• 初始化后的w除以输入数据个数的平方根有利于收敛。

• $Var(XY) = [E(X)]^2Var(Y) + [E(Y)]^2Var(X) + Var(X)Var(Y)$

• biases通常初始化为0

• 实践中若采用ReLU激活函数，通常使用w=np.random.randn(n)*sqrt(2.0/n)进行初始化。

• 神经网络使用Batch Normalization是常见的事

5.正则化

• L2正则化：使得w不会太大

• L1正则化：使得w尽可能接近0

• Max norm constraints: 限定w长度的最大值，即$

  w

  _2 \lt c$

• Dropout:训练过程中以概率p删除神经元节点，在预测过程中需要对采用dropout的隐层结果乘以p（Inverted dropout不需要，推荐使用）。

  Dropout: A Simple Way to Prevent Neural Networks from Overfitting

  Dropout Training as Adaptive Regularization

• In practice: It is most common to use a single, global L2 regularization strength that is cross-validated. It is also common to combine this with dropout applied after all layers. The value of p=0.5p=0.5 is a reasonable default, but this can be tuned on validation data.

6.损失函数

• hinge loss、softmax loss
• 当类别很多时，可以采用Hierarchical Softmax
• 如果有可能，尽可能把回归问题转换成分类问题（离散化），因为L2 loss比softmax更难优化且一个离群点会引入更大的梯度。如果不得已使用回归，则使用dropout不是一个好主意，尤其是在L2 loss前一层使用。

7.Learning

• Gradient checks:

  $\frac{df(x)}{dx} = \frac{f(x+h) - f(x)}{h} \tag 1$

  $\frac{df(x)}{dx} = \frac{f(x+h) - f(x-h)}{2h} \tag 2$

  通常使用(2)做Gradient checks，因为(2)更精确。通过泰勒展开可以知道(2)的误差为$O(h^2)$的高阶无穷小，而(1)的误差为$O(h)$的高阶无穷小。$h$通常设为1e-4 ~ 1e-6。仅对每个参数检查少量维数的梯度。

  等到发现loss确实是下降的再做梯度检查！

  为了防止梯度检查中data loss 被 regularization loss掩盖，先不加入regularization loss 进行Gradient checks，然后再将其加入进行Gradient checks。同时，在Gradient checks时不使用Dropout和Data augmentation

  ?: Therefore, a better solution might be to force a particular random seed before evaluating both f(x+h) and f(x−h), and when evaluating the analytic gradient.

• 使用相对差来比较数值梯度与解析梯度，即$$\frac{

  f_a’ - f_n’

  }{\max(

  f_a’

  ,

  f_n’

  )}$$，因为当$f_n’$和$f_a’$很小的时候使用分子来比较不合理。

  • relative error > 1e-2 usually means the gradient is probably wrong

  • 1e-2 > relative error > 1e-4 should make you feel uncomfortable

  • 1e-4 > relative error is usually okay for objectives with kinks. But if there are no kinks (e.g. use of tanh nonlinearities and softmax), then 1e-4 is too high.

  • 1e-7 and less you should be happy.

  • 但是需要注意，神经网络越深，相对差越大，例如对于一个10层的神经网络，1e-2的相对差是可以接受的。

  • 计算相对差的时候使用double类型的浮点数，float类型会使得相对差变大。

    What Every Computer Scientist Should Know About Floating-Point Arithmetic

    在梯度检查的时候我们中途打印梯度更有利于检查。

• Sanity Check

  • 检查初始的loss是否正确，先不加正则化项，正确后再加入正则化项检测。
  • 在小数据集上训练，将其data loss训练到接近0(overfit)。这样能保证一般情况下正确，比如在特征是随机的情况下尽管overfit但是并不正确。

• 监视训练过程

  • 作图时，使用epoch（每个样例都被访问过一次为一个epoch）作为横坐标比iterations好，因为iterations取决于batch size的大小。

  • 学习率：

    

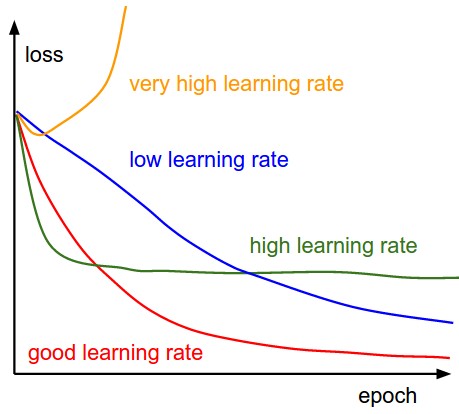
  • batch size 太小会使得loss曲线震荡下降

  • 训练集精度与验证集精度：

    

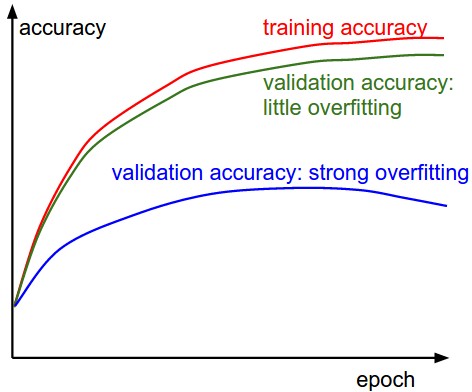
    绿色曲线说明模型容量小，可以增加神经网络参数来调整。

  • Ratio of weights: 参数更新量的值(np.linalg.norm(-learning_rate*dW))和参数本身(np.linalg.norm(W.ravel()))的比，这个值通常在1e-3左右。大于1e-3说明学习率大了，否则学习率小了。

  • 检测不好的初始化：统计激活值与梯度的直方图，观察它们的分布。

  • 可视化第一层特征，如果是光滑、清晰的说明很好

• 参数更新

  • momentum(相当于物体运动过程中的动摩擦因素？):

    1
    2
    v = mu*v - learning_rate*dx
    x += v
    

    ​

  • Nesterov Momentum（没看明白(2)的写法）:

    (1):

    1
    2
    3
    x_ahead = x + mu * v
    v = mu * v - learning_rate * dx_ahead
    x += v
    

    (2):

    1
    2
    3
    v_prev = v
    v = mu * v - learning_rate * dx
    x += -mu * v_prev + (1 + mu) * v
    

    推荐阅读：

    • Advances in optimizing Recurrent Networks by Yoshua Bengio, Section 3.5.
    • Ilya Sutskever’s thesis (pdf) contains a longer exposition of the topic in section 7.2

  • Annealing the learning rate(有三种方式):

    • step decay: 随着epoch增加，减小学习率。实践中可以查看验证集精度，如果验证集精度不再提高，可以适当降低学习率。
    • Exponential decay: $\alpha = \alpha_0e^{-kt}$，其中$\alpha_0, k$是超参数，t是迭代次数或者轮数。
    • 1/t dacay: $\alpha = \alpha_0 /(1 + kt)$，其中$\alpha_0, k$是超参数，t是迭代次数或者轮数。

    实践中采用step decay多一点，因为k这个参数不太好解释。

  • 其他优化方法：

    • 牛顿法： $x \leftarrow x - [Hf(x)]^{-1}\nabla f(x)$ ，其中$Hf(x)$是Hessian 矩阵（一个二阶偏导数矩阵），该方法由于没有学习率等超参数，因此得到一些人的支持。不过这个方法在深度学习中是无法使用的，因为深度学习的参数通常有百万个，计算Hessian矩阵的时间和空间开销都非常大。因此，有人提出了求Hessian矩阵逆的估计值，其中最好的是L-BFGS ，这样尽管Hessian矩阵求出来了(存储问题解决了)，但是原始的L-BFGS必须在整个训练集上计算，而训练集通常很大。

    实践中不常用L-BFGS，通常采用SGD+Nesterov Momentum.

    推荐阅读：

    • Large Scale Distributed Deep Networks is a paper from the Google Brain team, comparing L-BFGS and SGD variants in large-scale distributed optimization.
    • SFO algorithm strives to combine the advantages of SGD with advantages of L-BFGS.

  • 对每个参数设置自适应的学习率：

    Adagrad、RMSprop、 Adam(常用)

    Unit Tests for Stochastic Optimization proposes a series of tests as a standardized benchmark for stochastic optimization

  • 超参数优化

    贝叶斯超参数优化:Hyperparameter search, Bayesian optimization and related topics

8.评估

• 模型集成

  • 同样的模型，不同的初始化
  • 在交叉验证中发现的最好的几个模型
  • 单个模型的不同检测点(???)
  • 在训练过程中，取最后几个epoch得到的权重取平均

  相关阅读： “Dark Knowledge”

推荐阅读：

• SGD tips and tricks from Leon Bottou
• Efficient BackProp (pdf) from Yann LeCun
• Practical Recommendations for Gradient-Based Training of Deep Architectures from Yoshua Bengio

---

• ← Previous Post
• Next Post →